LE GMEAN (suite) 2
Vous trouverez ci-dessous la copie du fichier optimalf.xls de Gibbons:
Vous constaterez que c'est l'application pratique à une spéculation sur les futurs du système.
Le nombre de trades est la partie entière de la division du compte par la somme nécessaire pour se placer sur un trade.
Cette somme nécessaire pour trader un contrat est égale à la perte maximale ( -6.54 )* $625/-0.36= 11 354.17.
Toutes ces données permettent de calculer le tableau:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Num |
Trades |
HPRs |
# Units |
Acct. Equity |
|
|
|
|
|
(points) |
Traded |
100 000 |
||
|
Current f |
f |
0,36 |
|
1 |
9,15 |
1,50 |
8 |
145 750 |
|
Starting Acount Equity |
Start |
$100 000 |
|
2 |
5,90 |
1,32 |
12 |
190 000 |
|
Dollars per whole point per unit |
Dollars |
$625 |
|
3 |
1,20 |
1,07 |
16 |
202 000 |
|
Largest losing trade (points) |
MaxLoss |
-6,54 |
|
4 |
-4,20 |
0,77 |
17 |
157 375 |
|
Equity required per unit traded |
EPU |
$11 354,17 |
|
5 |
-5,05 |
0,72 |
13 |
116 344 |
|
Terminal Wealth Relative |
TWR |
7,1482 |
|
6 |
-3,70 |
0,80 |
10 |
93 219 |
|
Number of trades |
Num.Trades |
49 |
|
7 |
0,65 |
1,04 |
8 |
96 469 |
|
Geometric mean |
GMEAN |
1,0410 |
|
8 |
2,10 |
1,12 |
8 |
106 969 |
|
Geometric average trade |
GAT |
$465,03 |
|
9 |
-1,45 |
0,92 |
9 |
98 813 |
|
Ending equity trading at current f |
EGAIN |
$658 256 |
|
10 |
15,80 |
1,87 |
8 |
177 813 |
|
|
|
|
|
11 |
4,20 |
1,23 |
15 |
217 188 |
|
|
12 |
8,55 |
1,47 |
19 |
318 719 |
|||
|
|
13 |
-2,70 |
0,85 |
28 |
271 469 |
|||
|
|
14 |
13,54 |
1,75 |
23 |
466 106 |
|||
|
|
15 |
-1,74 |
0,90 |
41 |
421 519 |
|||
|
|
16 |
-2,12 |
0,88 |
37 |
372 494 |
|||
|
|
17 |
14,92 |
1,82 |
32 |
670 894 |
|||
|
|
18 |
-2,88 |
0,84 |
59 |
564 694 |
|||
|
|
19 |
2,32 |
1,13 |
49 |
635 744 |
|||
|
|
20 |
-3,16 |
0,83 |
55 |
527 119 |
|||
|
|
21 |
-0,92 |
0,95 |
46 |
500 669 |
|||
|
|
22 |
-3,14 |
0,83 |
44 |
414 319 |
|||
|
|
23 |
11,68 |
1,64 |
36 |
677 119 |
|||
|
|
24 |
3,32 |
1,18 |
59 |
799 544 |
|||
|
|
25 |
0,56 |
1,03 |
70 |
824 044 |
|||
|
|
26 |
-6,00 |
0,67 |
72 |
554 044 |
|||
|
|
|
|
|
27 |
1,08 |
1,06 |
48 |
586 444 |
|
|
|
|
|
28 |
-5,84 |
0,68 |
51 |
400 294 |
|
|
|
|
|
29 |
-1,50 |
0,92 |
35 |
367 481 |
|
© Copyright 1994 |
|
|
30 |
6,08 |
1,33 |
32 |
489 081 |
|
|
by Gibbons Burke |
|
|
31 |
2,00 |
1,11 |
43 |
542 831 |
|
|
All rights reserved |
|
|
32 |
-4,58 |
0,75 |
47 |
408 294 |
|
|
|
|
|
|
33 |
2,98 |
1,16 |
35 |
473 481 |
|
|
|
|
|
34 |
-0,64 |
0,96 |
41 |
457 081 |
|
|
|
|
|
35 |
4,22 |
1,23 |
40 |
562 581 |
|
|
|
|
|
36 |
21,06 |
2,16 |
49 |
1 207 544 |
|
|
|
|
|
37 |
-6,54 |
0,64 |
106 |
774 269 |
|
|
|
|
|
38 |
-0,22 |
0,99 |
68 |
764 919 |
|
|
|
|
|
39 |
-3,06 |
0,83 |
67 |
636 781 |
|
|
|
|
|
40 |
-3,12 |
0,83 |
56 |
527 581 |
|
|
|
|
|
41 |
2,20 |
1,12 |
46 |
590 831 |
|
|
|
|
|
42 |
14,06 |
1,77 |
52 |
1 047 781 |
|
|
|
|
|
43 |
-2,16 |
0,88 |
92 |
923 581 |
|
|
|
|
|
44 |
3,44 |
1,19 |
81 |
1 097 731 |
|
|
|
|
|
45 |
4,12 |
1,23 |
96 |
1 344 931 |
|
|
|
|
|
46 |
-5,24 |
0,71 |
118 |
958 481 |
|
|
|
|
|
47 |
-2,96 |
0,84 |
84 |
803 081 |
|
|
|
|
|
48 |
-0,86 |
0,95 |
70 |
765 456 |
|
|
|
|
|
49 |
-2,56 |
0,86 |
67 |
658 256 |
La partie droite de la feuille de Gibbons reproduit: l'optimal f, le gmean correspondant ainsi que le résultat de la spéculation qui en résulte:
f = 0.12 -> gmean = 1.02 -> résultat total des trades = 255 119
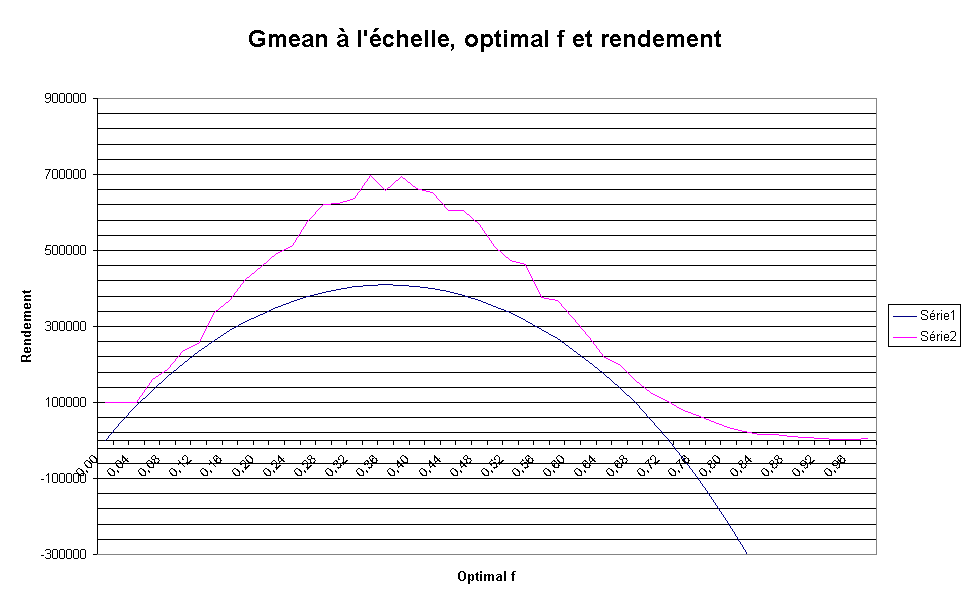
Vous trouverez quelques graphiques permettant de visualiser ces données.
Deux points sont à mettre en évidence:
1- Par rapport à l'axe de symétrie du gmean,pour un même rendement, il est préférable de choisir l'optimal f le plus faible.
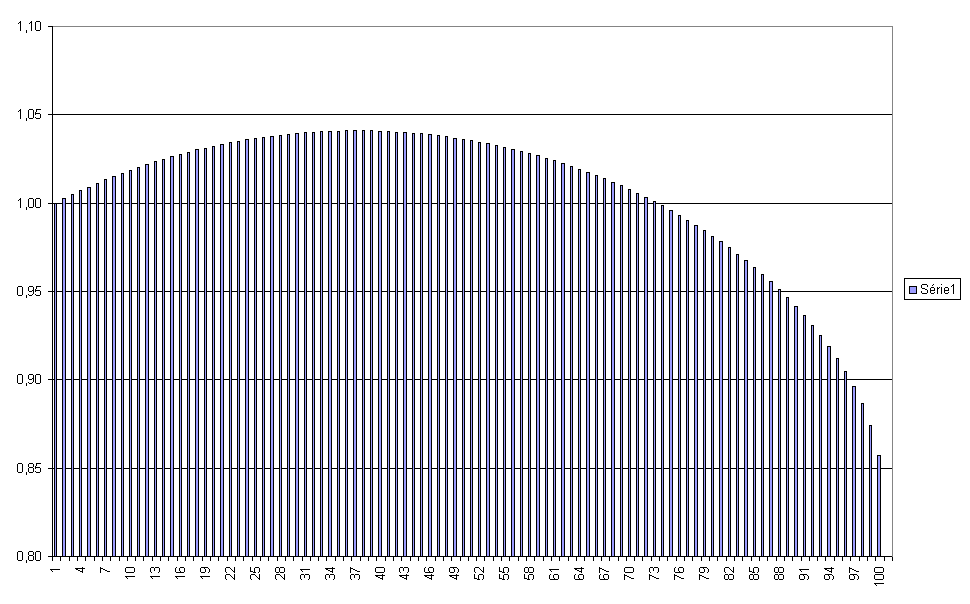
2- En observant le graphique ci dessous, on se rend compte que le sommet du graphe est très aplati, et que l'on peut arbitrer sans trop de dommages pour un optimal f légèrement plus faible.